勾股定理的逆定理:若一个三角形的三边满足关系式a²+b²=c²,则这个三角形为直角三角形。
题目1:如图1,在三角形ABC中,满足AC ²+BC ²=AB ²。求证:∠ACB=90°。

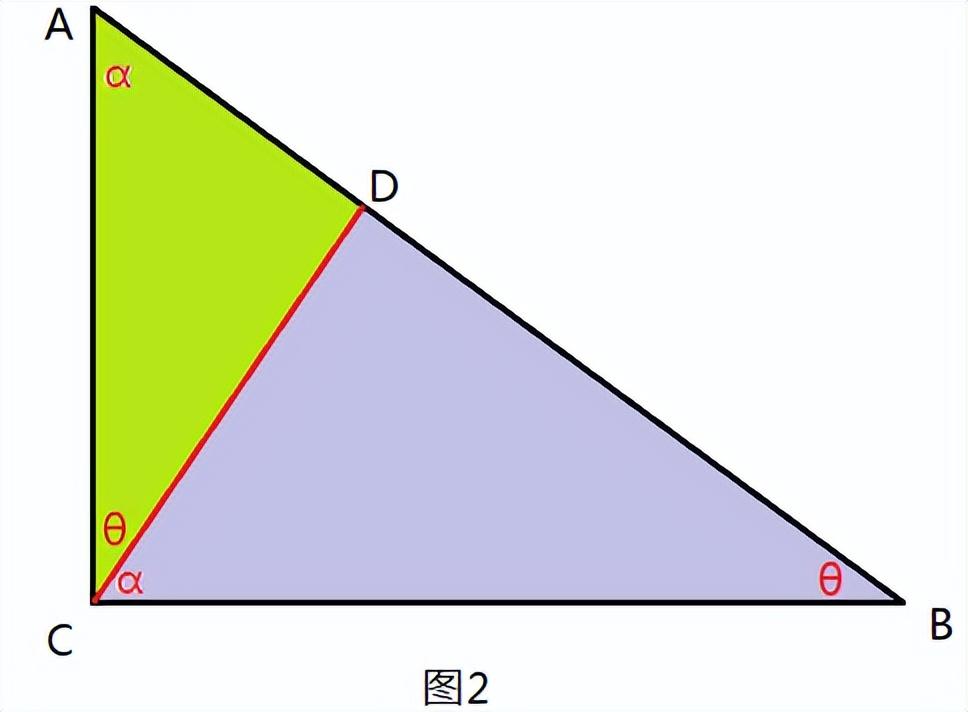
解题思路:在AB上取点D,使∠DCB=∠A=α(图2)。
易证△CBD∽△ABC(母子型相似),
CB²=BD·BA…………①。
已知AC ²+BC ²=AB ²,将①代入:
AC ²+ BD·BA=AB ²,
AC ²+(BA-AD)·BA=AB ²,化简得:
AC ²=AB·AD,即AC/AD=AB/AC,
△ADC∽△ACB,则∠ACD=∠ABC=θ。
在△ABC中,2α+2θ=180°,
α+θ=90°,即∠ACB=90°。
题目2:判断三边长分别为2n²+2n,2n+1, 2n²+2n+1(n>0)的三角形是否是直角三角形?
解题思路:利用勾股定理的逆定理来判断。
其中两边长的平方和是:
(2n²+2n)²+(2n+1)²=(2n²+2n)²+4n²+4n+1;
第三边的平方为:
(2n²+2n+1)²=(2n²+2n)²+2(2n²+2n)+1
=(2n²+2n)²+4n²+4n+1。
则(2n²+2n)²+(2n+1)²=(2n²+2n+1)²,
故边长为2n²+2n,2n+1, 2n²+2n+1的三角形是直角三角形。
题目3:三角形三边边长a、b、c满足a ²+b ²+c ²+338=10a+24b+26c。证明:△ABC是Rt△。
解题思路:将已知等式变形:
a ²+b ²+c ²+338=10a+24b+26c,
a ²-10a+25+b ²-24b +144+c ²-26c+169=0,
(a-5)²+(b-12)²+(c-13)²=0,
(a-5)²=0,a=5
(b-12)²=0,b=12
(c-13)²=0,c=13,
即△ABC的边长分别为5、12、13,为一组勾股数,故△ABC为直角三角形。
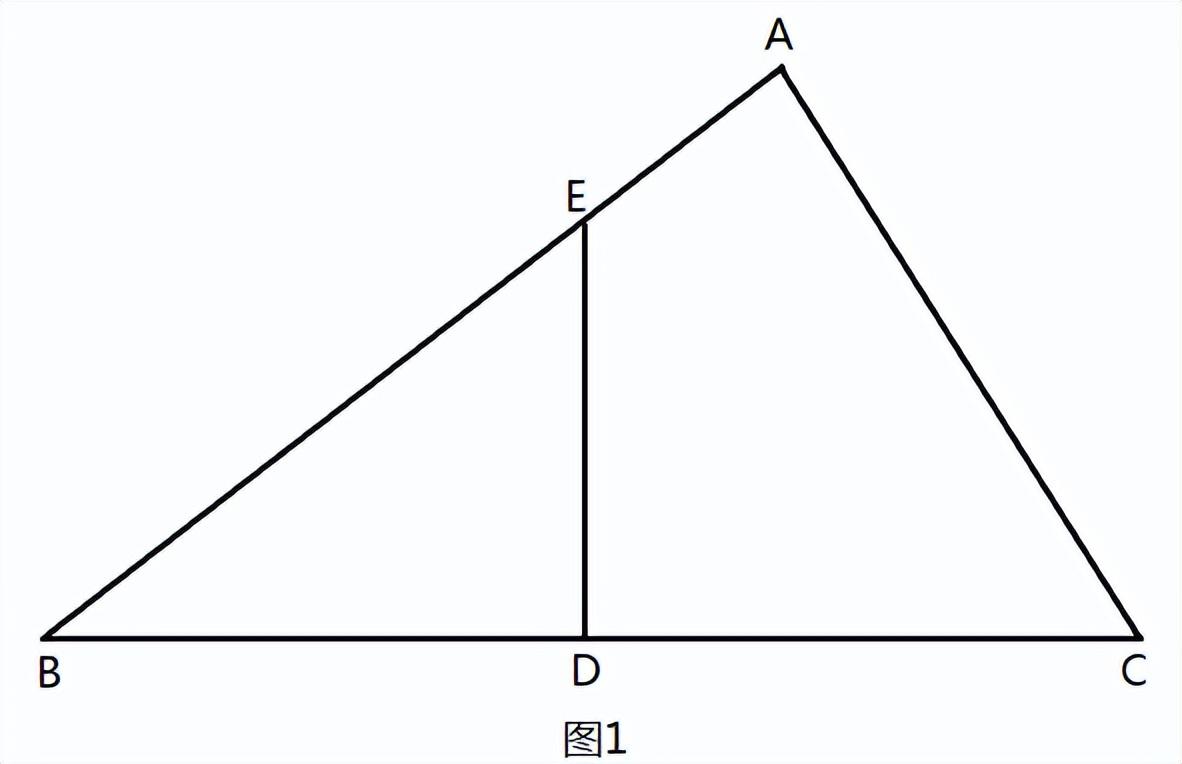
题目4: 如图1,在△ABC中,D是BC的中点,ED⊥BC,垂足为D,ED交AB于点E,且BE ²-EA ²=AC ²。证明:∠A=90°。
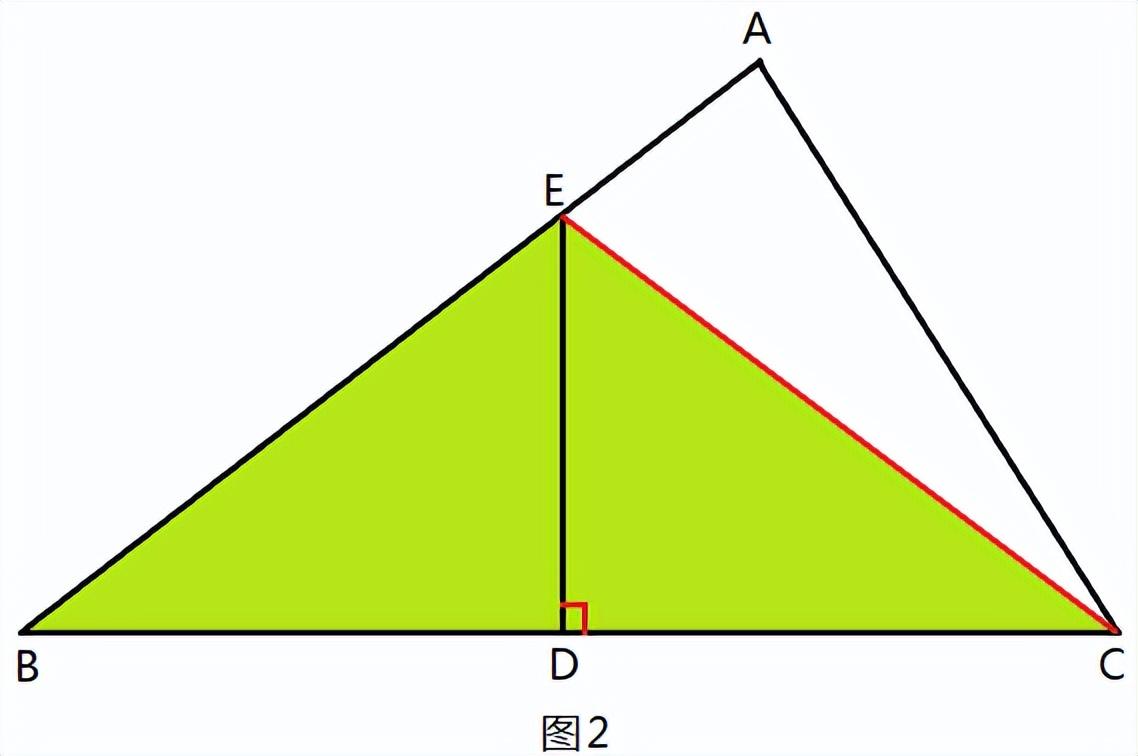
解题思路:连接EC(图2),已知ED为BC的垂直平分线,故BE=EC。
有知BE ²-EA ²=AC ²,即EC²-EA ²=AC ²,变形为:
EA ²+AC ²= EC²,根据勾股定理的逆定理,
△EAC为Rt△,∠A=90°成立。
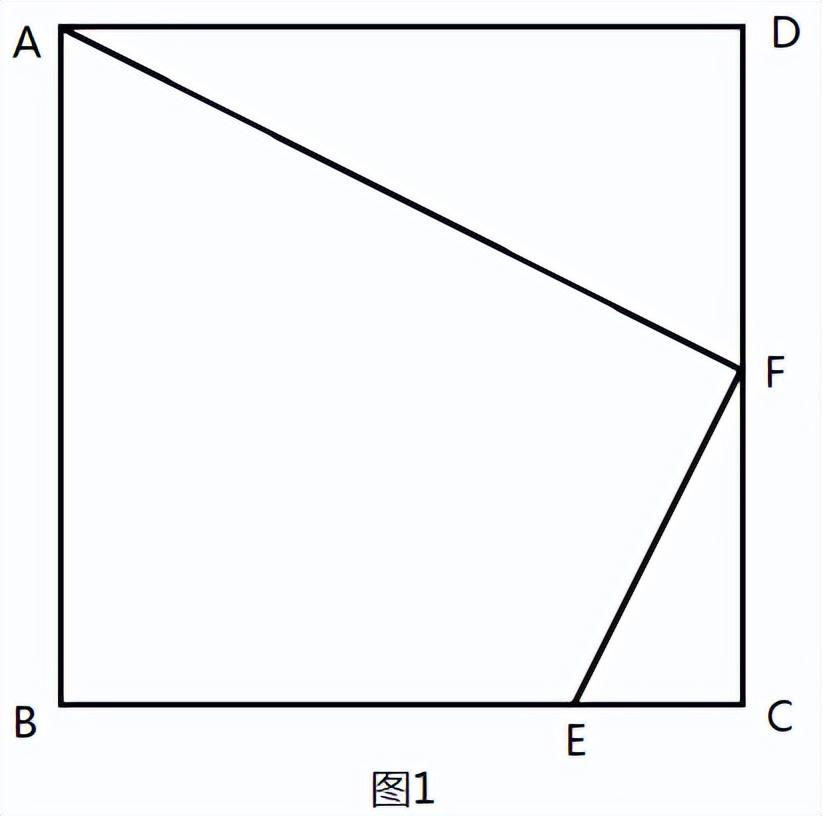
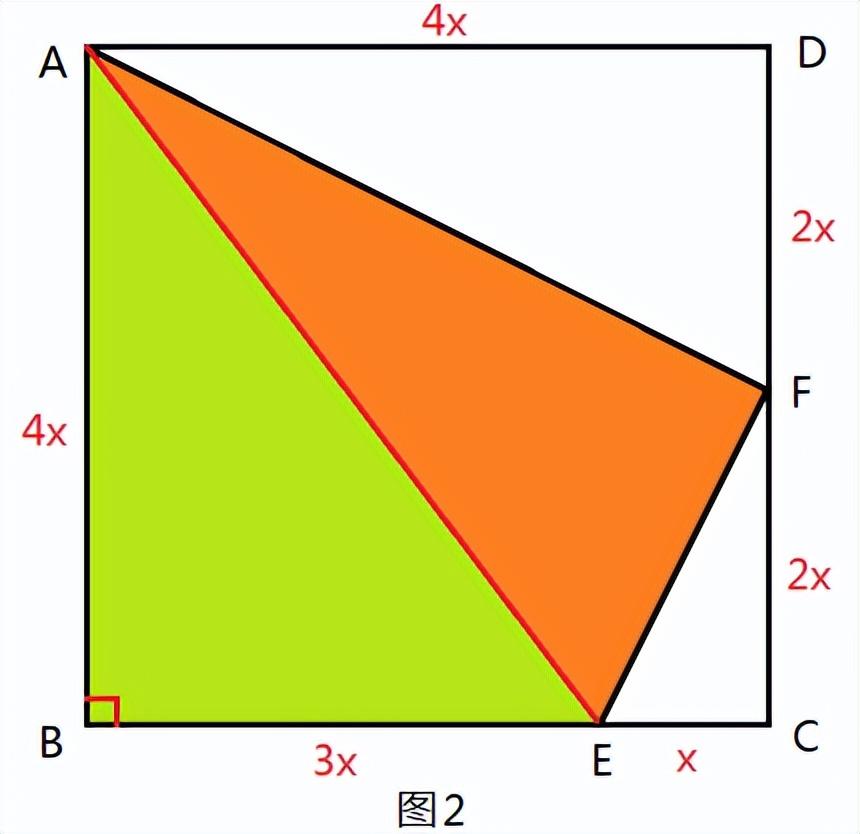
题目5:如图1,在正方形ABCD中,F是DC的中点,EC=1/4 BC。求证:EF⊥AF。
解题思路:连接AE(图2),设EC=x,BE=3x,
FC=FD=2x,AB=AD=4x。
在Rt△ABE中,
AE²=AB²+BE²=(4x)²+(3x)²=25x²;
AF²+EF²=AD²+DF²+EC²+FC²
=(4x)²+(2x)²+x²+(2x)²=25x²,
故AF²+EF²= AE²,根据勾股定理的逆定理,
△AFE为Rt△,EF⊥AF成立。
题目6:如图1,四边形ABCD为圆内接四边形,AB与BC的平方和等于CD与AD的平方和,证明AC为圆的直径。

解题思路:欲证AC为圆的直径,证明∠ADC或∠ABC为90°即可。
延长AD、BC交于E点(图2),设AB=x,BC=y,CD=m,AD=n,CE=a,DE=b。
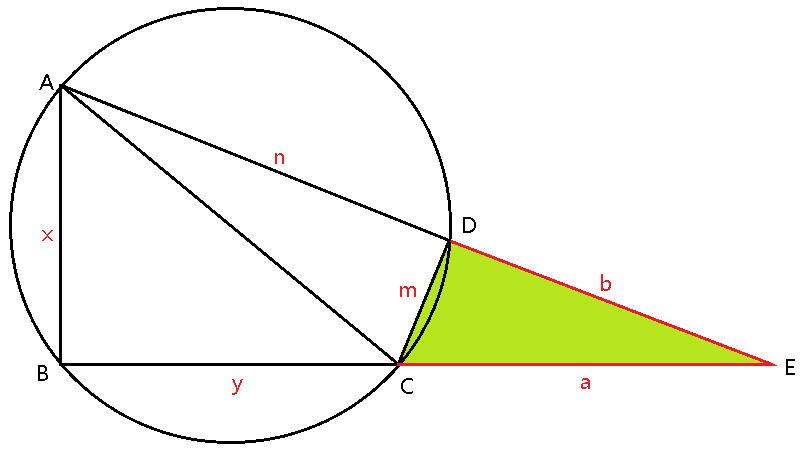
图2
易证△EDC∽△EBA,b/(y+a)=a/(n+b) =m/x。得出下列2式:
bx=m(y+a)=my+ma……①
ax=m(n+b)=mn+mb……②
由①+②:x(a+b)=m(n+y)+m(a+b)
(a+b)(x-m)= m(n+y) ……③
由②-①:x(a-b)=m(n-y)+m(b-a)
(a-b)(x+m)= m(n-y)……④
由③x⑷:(a ²-b ²)(x ²-m ²)=m ²(n ²-y ²)
已知x ²+y ²=m ²+n ²,x ²-m ²= n ²-y ²
所以a ²-b ²=m ²
a ²=m ²+ b ²,△CDE为直角三角形,∠ADC=∠CDE=90°,
故AC为圆的直径。
