前面已经介绍了很多标准九宫数独的技巧,能解决大部分三星难度以下的题目,但是在做三星以上的题目时,会发现单纯的使用摒除法(包含宫摒除、行列摒除等)和唯一余数法无法解决有些题目,这是就需要用到更多的技巧了,今天我们来介绍非常常见的一种方法——区块法(不是最近热炒的区块链哦,哈哈),所谓区块法,就是指某一区块(某宫的某些单元格或者某行列的单元格或者其他几个单元格)能确定填某一个或某几个数字时,这样这些行列宫里就不能填写这些确定的数字,从而完成数独的一种方法。区块法一般可以分为宫区块、行列区块、组合区块等,今天先介绍宫区块法。
我们还是一样从具体的题目入手,介绍宫区块法,看题:
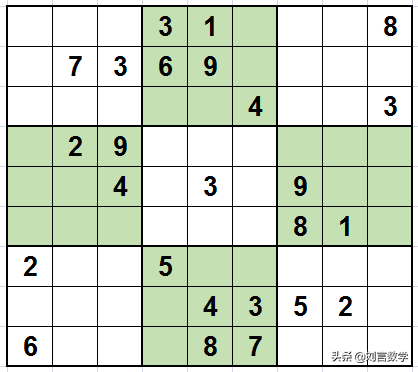
首先,我们使用摒除法和唯一余数法,看看能填出多少个数字。
仔细观察,如图所示,2的宫摒除法,可以确定第九行第四列填2.
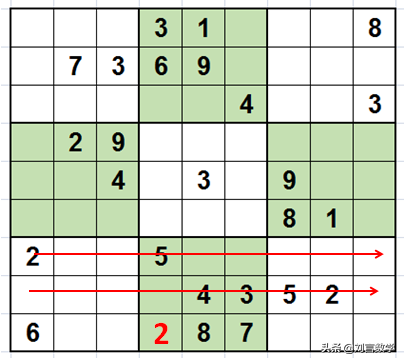
继续使用宫摒除法,可以发现,如图所示,8的宫摒除法可以确定第七行第八列填8.
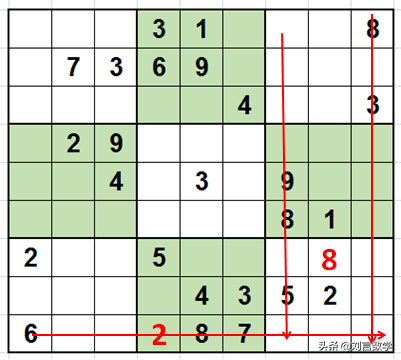
之后我们就发现使用摒除法和唯一余数法无法继续确定其他的数字了,该今天的主角登场了。
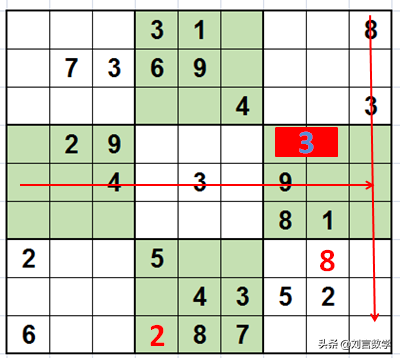
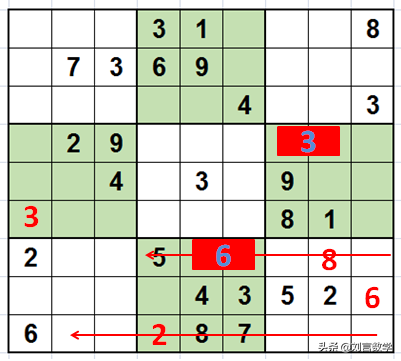
观察数字3,在使用宫摒除时,我们可以看到:
虽然第六宫的3不能确定在哪一个单元格,但是可以知道这两个单元格必有数字3,也就意味着第四行其他的位置不能出现3,如图所示:(我们用如图所示的方法表示这个区块一定填3)
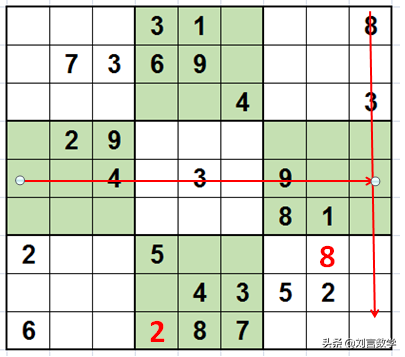
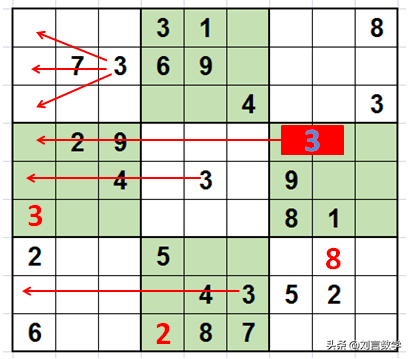
继续观察第一列的3,如图所示:

采用列摒除法,可以得出第一列的3出现在第六行第一列。
在做6的摒除法时,我们可以发现:
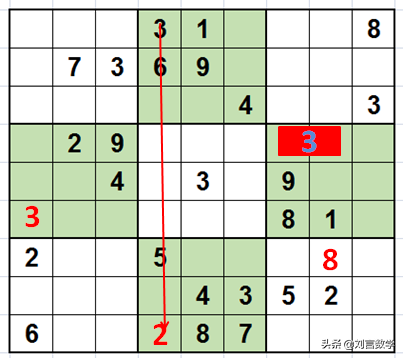
第八宫的第七行的两个单元格一定有一个填6,如图所示:
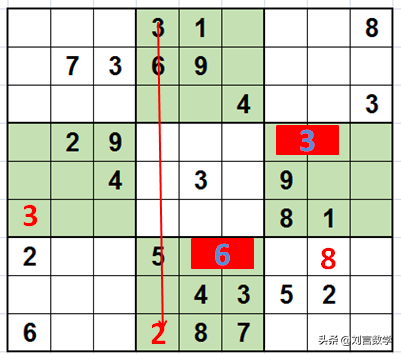
因此第九宫的6就确定位置了。
通过这两个数字的填法,亲爱的读者们,你们明白了宫区块法了吗?
